Math plays a big role in case interviews because it helps you solve business problems logically and in a structured way. It’s not about applying complex formulas; it’s about working quickly with numbers and finding practical solutions. Since you won’t have a calculator and can only use pen and paper, knowing effective calculation methods is key. These skills show off your analytical mindset and can make you stand out from other candidates.
Why Mental Math is a Big Plus
In case interviews, being able to handle basic calculations in your head is a huge advantage. It saves time and makes you appear more flexible and confident. It’s not about avoiding writing things down entirely, it’s rather about quickly grasping the results. The goal is to get a fast overview and deliver precise answers. Imagine calculating revenue and profit for multiple products – if you can confidently do these calculations in your head, you’re already a step ahead.
Working with Rounded Numbers
In case interviews, you’ll often see “rounded” numbers like 300,000 or 4,000,000. Working with large numbers can feel intimidating, but a few simple tricks can make it much easier.
💡 Quick Trick: Cutting Zeros
Let’s say you’re calculating the revenue for a product that a company sells at $32 per unit, with 25,000 units sold annually. The calculation is 32 × 25,000. Instead of writing all those zeros, break it into simpler steps:
- Calculate 32 × 25 first, which is easier than 32 × 25,000.
- Then, just add the three zeros from “25,000” to the result.
To quickly solve 32 × 25, you can think of 25 as ¼ × 100:
- 32 × ¼ = 8
- 8 × 100 = 800
So, 32 × 25 is 800, making 32 × 25,000 equal to 800,000. This method saves time and reduces the chance of misplacing zeros.
Adding and Subtracting with Units
Large numbers, like 250 million or 300 million, might seem challenging at first glance. A useful technique is to work with units like thousands (K), millions (M), billions (B), and trillions (T). This simplifies addition or subtraction because you don’t have to write out or imagine all the zeros.
💡 Quick Trick: Adding Large Numbers
Suppose you need to add 250 million, 300 million, and 150 million. Instead of writing each number fully, just add the leading numbers and keep the unit:
- 250 + 300 + 150 = 700, then add the “million” unit.
"The result is 700 million. This approach is quicker and reduces errors since you’re focusing only on the main numbers, not all the extra zeros.
Multiplication and “Clean Numbers”
Multiplication is common in case interviews, and many numbers used are “clean numbers”, meaning they have helpful properties that make calculations easier. For example, 25 is a “clean” number because it’s ¼ × 100, which simplifies large multiplications.
💡 Quick Trick #1: Fast-Math Multiplication:
The Fast-Math Method is a technique for simplifying complex multiplications by breaking them into easier steps. It’s based on the idea that you can halve one number and double the other without changing the result, thanks to the commutative property of multiplication. This keeps the final product the same but often makes the math easier. Here’s an example:
Original calculation: 160 × 350
- Halve 160: 160 ÷ 2 = 80
- Double 350: 350 × 2 = 700
- Multiply the results: 80 × 700 = 56,000
The result is the same as 160 × 350 but without lengthy calculations. This method is especially handy in case interviews, allowing for quick, error-free calculations.
💡 Quick Trick #2: Reordering Multiplication Factors:
Another helpful technique is rearranging terms to make the multiplication easier. Imagine you need to calculate 125 × 2.5 × 4. You can rearrange like this:
- Start with 125 × 4 = 500.
- Then, 500 × 2.5 = 1,250.
The answer is 1,250. Reordering simplifies the calculation. You could also do 2.5 × 4 = 10, then 125 × 10 = 1,250. This flexibility lets you choose the easiest order for each case.
Quick Calculations for Percentage Growth
Let’s say a company grows 4% per year. Calculating this over multiple years can often be simplified by ignoring compound interest and estimating growth. This is especially helpful for shorter time periods and moderate growth rates.
Example: Estimating Percentage Growth
If a company’s revenue is $400 million and it grows at 4% annually for six years, you can estimate the growth like this: 4% × 6 = 24%, which is roughly one-quarter. So the revenue grows by about 25%, or around $100 million, bringing it to about $500 million after six years. This method gives a quick estimate for growth impact over several years.
The Net Present Value (NPV) Method
The Net Present Value (NPV) method is a common approach to calculate the current value of a future investment. It helps determine today’s value of expected cash flows by discounting future payments. A positive NPV indicates a worthwhile investment, as future returns exceed the initial cost.
💡 Quick Trick: Rule of 72
The “Rule of 72” is a tool for estimating the doubling time of an investment—how long it’ll take to double in value. The Rule of 72 uses the exponential growth formula and can be applied when a rate of return (or growth rate) is known.
Simply divide 72 by the annual interest rate (in percent) to estimate the doubling time. For example, if the growth rate is 6% annually, the investment doubles in about 12 years (72 ÷ 6 = 12).
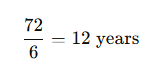
This quick estimation helps estimate the future value of an investment without needing to apply the exact NPV formula. Since it’s an approximation, it’s great for quick decisions or rough estimates but less suited for precise calculations.
Example: NPV of a Real Estate Project
A real estate company is considering a project that will sell apartments for $250 million in six years. What’s the current value of this investment if they expect a 12% return annually? Using the Rule of 72, an investment with a 12% growth rate doubles in about six years (72 ÷ 12 = 6). So, today’s value is roughly half the future value, or $125 million. This means the company should invest no more than $125 million to achieve a 12% return.
Conclusion
Math and quick calculations are essential in case interviews to help you stand out from other candidates. The methods and examples here allow you to tackle common calculations efficiently and accurately. From working with rounded numbers to using the Fast-Math Method, these techniques make you faster and more confident with numbers. Practice these methods before your interview to be flexible and confident, showcasing your math skills effectively.

