Net Present Value - NPV

Net Present Value (NPV) is the sum of all discounted future cash flows of a project or investment. These discounted cash flows are referred to as Present Values (PVs). NPV allows us to calculate the current value of money to be received or paid at different points in the future, helping determine the profitability of an investment. If the NPV is positive, the project generates value. A negative NPV, on the other hand, suggests a loss.

The Time Value of Money – An Intuitive and Financial Explanation

The time value of money reflects the principle that money today is worth more than the same amount in the future because it can be invested and earn interest. There are two ways to explain this concept:

• Intuitive Explanation: People prefer to have money now rather than later because it involves less risk. For example, would you rather have €100 today or in a year? Most would choose today, as future payments come with uncertainty, like inflation or the risk of default.

• Financial Explanation: If you have €100 today, you could invest it at a 2% interest rate and have €102 in a year. To find the present value of €102 in one year, you divide it by 1.02, which gives you €100. This shows how future cash flows are discounted to their present value.

   

Calculating Net Present Value (NPV)

NPV is calculated as the sum of all discounted future cash flows. The present value (PV) of a single future cash flow is given by the following formula:

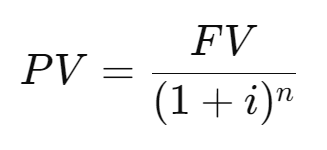
• PV: Present value of a future cash flow
• FV: Future value of the cash flow
• i: Discount rate or interest rate per period
• n: Number of periods between now and the future cash flow

The Net Present Value (NPV) is the sum of all these present values (PVs) for the project's future cash flows:

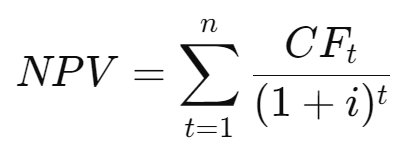
• CF_t: Cash flow in year t
• i: Discount rate
• n: Number of periods

If the NPV is positive, the discounted cash flows exceed the initial investment, indicating the project is profitable. A negative NPV suggests that the project will result in a net loss.

Example of NPV Calculation

Let’s say you receive €102 in one year and €102 in two years with a discount rate of 2%. The present value of the first cash flow is:

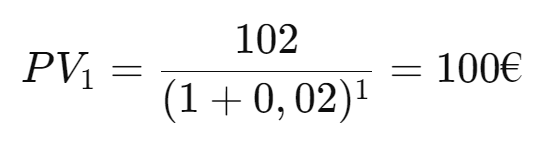
The present value of the second cash flow is:

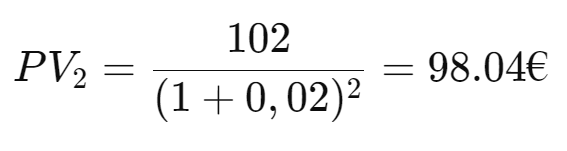
The total NPV of this investment is the sum of the present values:

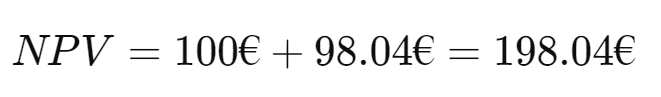
Applying the NPV in Case Interviews

In case interviews, it is unlikely that you will need to perform a complex NPV calculation, as such calculations can be time-consuming. However, there are some useful shortcuts and concepts that you can apply to argue effectively and efficiently.

NPV for Infinite Cash Flows

For infinite cash flows (perpetuity), where a company or investment generates constant profits over an indefinite period of time, a simplified NPV formula can be used:

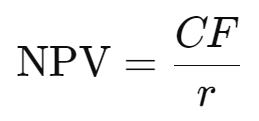
Here, CF stands for the constant annual cash flow and r for the discount rate.

Example: A company generates € 100 per year and the discount rate is 4%:

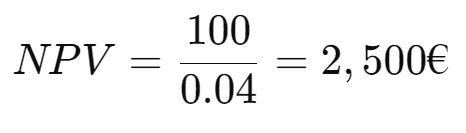
If the company grows at an annual rate of 2 %, the formula is as follows:

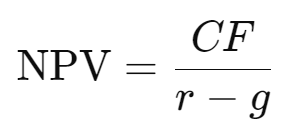
Where g stands for the growth rate.

Example calculation:

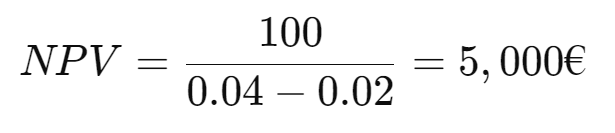
💡 Prep tip: In case interviews, you don't have a calculator to hand. To calculate the simplified version of the NPV calculation in your head, you should be able to do the basic types of calculation. Use our mental math tool to brush up on your skills!

Choosing the Right Discount Rate

Choosing the right discount rate is crucial for the NPV calculation. As a general rule, the greater the risk, the higher the discount rate.

Rule: Uncertain future income has a lower value. Therefore, discount rates between 1% and 3% are used for secure cash flows, while rates between 4% and 10% are common for most companies. For speculative start-ups, rates can even be as high as 40%. In case interviews, you can either ask directly for the discount rate or, if no specific information is available, use a rate of 10%.

Why Do Companies Use the NPV?

The NPV is an important tool for companies to assess the profitability of projects. A positive NPV indicates that future revenues exceed costs, while a negative NPV indicates that a project is not worthwhile.

Advantages of the NPV

• Accuracy: The NPV takes into account the time value of money and enables a precise assessment of future cash flows.
• Decision support: A company should only invest in a project if the NPV of the future cash flows is greater than the initial investment.
• Risk assessment: The ability to consider different scenarios through sensitivity analysis helps to make informed decisions.

Limitations of the NPV

Although the NPV is a useful tool, there are also some limitations. The NPV is based on assumptions, and incorrect assumptions can lead to erroneous results. Also, the consideration of secondary effects, such as synergy effects or effects on the corporate image, is often not taken into account in the NPV.

Example: A company plans to invest in a new production line, but assumes that the plant will be in operation for ten years. However, if demand for the product declines after just seven years, the originally calculated NPV may no longer apply.

Ready to apply the NPV yourself in a practical example? Try it out in this case!

Conclusion

• The NPV evaluates investments by discounting future cash flows to today's value.
• It makes it possible to compare projects with different cash flows and helps to make well-founded investment decisions.
• Sensitivity analyses are important for evaluating different scenarios, as the NPV depends heavily on the assumptions made.
• Secondary effects, such as synergies or image gains, are not taken into account in the NPV.